2019-05-03

フーリエ〇〇をまとめてみた

こんにちは、きぐまだ。

デジタル信号処理の勉強をしているとふと、「あれ、フーリエ〇〇って何するんだっけ」となってしまうことがあるので、見たときにすぐ思い出せるように自分なりにまとめてみた。

公式の詳しい導出はこの記事では言及しないことにする。詳しく知りたい方は一番下の参照まで。

フーリエ級数
フーリエ変換
離散時間フーリエ変換
離散フーリエ変換
おわりに
引用・参照

フーリエ級数

公式

$\displaystyle f(t) = a_0 + \sum_{k = 1}^{\infty} \left\{a_k \cos{ \left(\frac{2\pi k}{T_0} t\right) } + b_k \sin{ \left(\frac{2\pi k}{T_0} t\right) } \right\}$

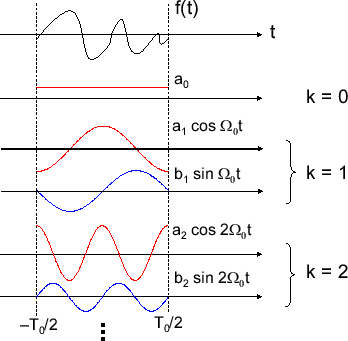
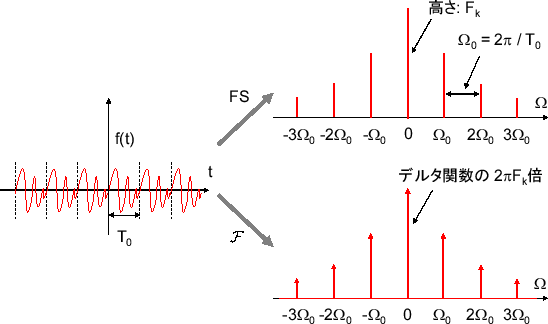
これは周期 $ T_0 $ の関数(信号)は角周波数が$ 2\pi / T_0 (= \Omega_0) $で自然数倍のsinとcosの足しあわせで構成されることを表している。$ a_0 $ は元の信号の振動しない成分だ。イメージは下の画像みたいな感じだ。

計算はしないのでフーリエ係数は省く。
フーリエ級数をオイラーの公式を用いて複素指数型で表すと、

公式

$\displaystyle f(t) = \sum_{k = -\infty}^{\infty} F_k e^{ j \Omega_0 k t}$

$\displaystyle F _ k = \frac{1}{T_0} \int_{-T_0 / 2}^{T_0 / 2} f(t) e^{-j\Omega_0 k t} dt$

$ F_k $ はこれのフーリエ係数を表している。
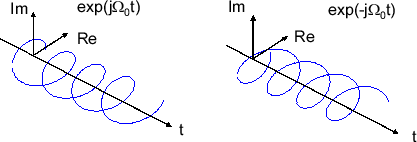
$ e^{ j\Omega_0 k t }$ は角周波数 $ \Omega_0 k$ の回転であり、反時計回りに時間と共に$ t $軸に進む。$ k < 0 $ の時は、時計回りに回転する。イメージは下の画像みたいな感じだ。

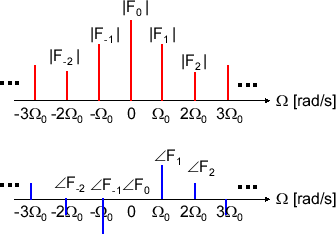
$ f(t) $ が実数だった場合、公式の複素数成分は無くならないといけない。つまり、$ F _ k e^{ j\Omega_0 k t}$と$ F _ -k e^{ -j\Omega_0 k t}$ の和が実数にならないといけない。よって $ |F _ k| = |F _ -k|$ の振幅が一致して、$ \angle F _ k = -\angle F _ -k $ の偏角の関係が成り立つ。フーリエ係数 $ F _ k $ が各周波数成分の振幅を表しているのでこちらのほうが直感的にわかりやすい。

フーリエ変換

公式

$\displaystyle f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(\Omega) e^{j \Omega t} d\Omega \ \ \ \ \ \ \ //フーリエ逆変換$

$\displaystyle F(\Omega) = \int_{-\infty}^{\infty} f(t) e^{-j \Omega t} dt \ \ \ \ \ \ \ //フーリエ変換$

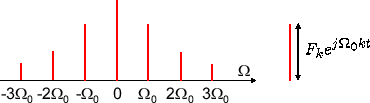
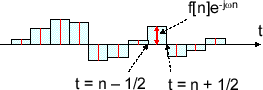
フーリエ逆変換は何となくフーリエ級数展開と似ていることがわかる。フーリエ級数展開では値が離散的だったが、面積として考え $ T_0 -> \infty$ すなわち $ \Omega_0 -> 0 $ としたものだ。そうすることで $ \Omega $ が連続化され積分で表せる。フーリエ変換も同様。面積のイメージは下の図みたいな感じだ。

　　　　　　　↓

そして、時間領域で周期的な $ f(t) $ をフーリエ変換すると、周波数領域ではデルタ関数が出てくる。これは周期関数を1周期だけ積分したフーリエ係数と違い、無限大まで積分するのでデルタ関数が出てくるのは必然だろう。周波数領域で見ると、フーリエ係数をフーリエ逆変換しても値を持たない。そこにデルタ関数をかけて面積を持つようにしてフーリエ逆変換すると、時間領域では信号が復元される。

離散時間フーリエ変換

公式

$\displaystyle F(\omega) = \sum_{n = -\infty }^{\infty} f[ n ] e^{-j\omega n} \ \ \ \ \ \ // 離散時間フーリエ変換$

$\displaystyle f[ n ] = \frac{1}{2\pi} \int_{-\pi}^{\pi} F(\omega) e^{j\omega n} d\omega \ \ \ \ \ \ // 離散時間フーリエ逆変換$

時間領域でただの離散的な値だと積分しても値が残らないので、先ほどのフーリエ逆変換と同じく面積として考えて総和を取ればよい。もしくは、離散的な値にデルタ関数をかけて値を持つようにすればよい。

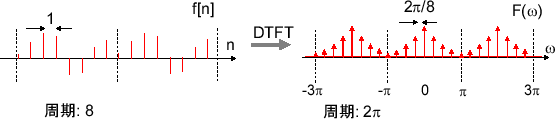
フーリエ変換では、離散的な周波数スペクトルは時間領域で連続だったが今回の場合、時間領域で離散的なので周波数スペクトルでは連続的になる。周期は $ 2\pi $ 。

周期的な周波数スペクトルをフーリエ逆変換すると、先ほど同様デルタ関数が出てくるので積分範囲は1周期だけにすると、離散時間フーリエ逆変換のようになる。だが、コンピュータが扱うことができるのはデジタル信号だけだ。そこで、周波数領域でも離散的な離散フーリエ変換が出てくる。

離散フーリエ変換

公式

$\displaystyle f[n] = \frac{1}{N} \sum_{k = 0}^{N - 1} F[ k ] e^{j \frac{2\pi}{N} k n} \ \ \ (n = 0 \cdots N-1) \ \ \ \ \ // 離散フーリエ逆変換$

$\displaystyle F[k] = \sum_{n = 0}^{N - 1} f[ n ] e^{-j\frac{2\pi}{N} k n} \ \ \ (k = 0 \cdots N - 1) \ \ \ \ \ // 離散フーリエ変換$

周期的ではない離散時間信号を離散時間フーリエ変換すると、周波数領域では周期 $ 2\pi $ の連続的なスペクトルになったが、時間領域で周期的だった場合、周波数領域では離散的になり、離散時間フーリエ変換では無限和とするので周波数領域ではデルタ関数が出てくる。

$ F(\omega) $ は

$\displaystyle F(\omega) = \sum_{k = -\infty}^{\infty} c _ k \delta(\omega - \frac{2\pi k}{N})$

と表せるから、離散時間フーリエ逆変換の式に突っ込んで色々変形すれば離散フーリエ逆変換が出てくる。

$ f[ n ] $ が周期的なとき、周波数領域ではデルタ関数が出てくるが、先ほど同様1周期分だけ総和を取ってしまえば値が無限にならなくて済む。つまり、$ \omega = 2\pi k / N $ の $ k = 0 \cdots N - 1 $ までの値が有限となって出る。これが離散フーリエ変換だ。

おわりに

どうしてこのような式になるのかを流れで理解するとそんなに難しいものではないことが分かった。

詳しい解説はぜひ参照から見てほしい。

引用・参照

・やる夫で学ぶディジタル信号処理(http://www.ic.is.tohoku.ac.jp/~swk/lecture/yaruodsp/main.html)

2019-04-16

「おしゃべりなコンピュータ」を読んだ

始めに

初めまして。kigma(きぐま)という者だ。

ボカロが好きな大学生だ。将来ボカロを超える音声合成を本気で作ろうとしているが、全くの初心者だ。最近、とあるきっかけがあって音声合成の勉強をし始めた。そして、自分の足跡を残すためにブログを始めた。長文を書くのが苦手であるから気になったことだけをまとめる。日本語が苦手なので文章に違和感があるかもしれないが温かい目で見て欲しい。

第一章　「コンピュータの声」に囲まれた私たちの日常

始めに、これを人間の声だと思ってなかっただろうか？(私は思ってた)

・バスや駅のアナウンス
・家電(お風呂とか)
・カーナビ etc.

実はこれ合成音声なのである。最近の技術って凄い(語彙力)。

これのメリットとしては、コストの削減と柔軟性に大きく関わってくる。

人間に喋らせるより、音声合成に喋らせたほうが人件費かからないから安く済む。しかも、テキスト打つだけだから急なアナウンスの変更に対応できる。まあテキストを考えるのは人間だが。

しかしそれすらも可能にすることができるのかもしれない。GoogleアシスタントやSiriや名古屋工業大学にあるメイちゃんなど、その片鱗を見せて活躍してるのがその例だ。

第二章　歌うコンピュータ

この章に紹介されてあった3つの音声合成技術についてここでまとめる。

フォルマント音声合成

母音は異なる周波数のサイン波の組み合わせによって構成されており、この複数の波のことをフォルマントという。このフォルマントや気道モデルなど、情報だけを元にあるルールに従い合成された音声だ。これは音声そのものを伝送することができなかった時代に、フォルマントの信号情報を圧縮して伝送していた「フォルマントボコーダー」が元になっている。

フォルマントで合成されているので会話はぎこちないらしい。

ダイフォン合成

これはボカロにも使われている技術で、人間の声を文字どおり2つの(=di)音素(=phone)で切り取ったもので合成された音声である。例えば、「あおい」という言葉であるなら、

「無音ーあ」

「あーお」

「おーい」

「いー無音」

の4ペアで切り取り、自然に繋げる。ピッチを上げたいときには、スペクトル包絡(今は言及しない)を保ったままにする。

私もボカロを使っているのでわかるが、かなり人間に近い歌声だとは思う。初めて喋らせたときは感動しすぎて涙が出そうになった。最近で言うと、ブラックホールが観測できたくらいに。

しかし、音声そのままを扱っているのでコストがかなり大きくなっていることや、感情の制御が困難であった。

HMM(隠れマルコフモデル)音声合成

これは名古屋工業大学が中心となって開発した技術で、簡単に言うと「人間が声を出す仕組みをシミュレートする」ということである。声を出す過程としてHMM音声合成では、

テキストが与えられる

　　　　　↓

HMMにより与えられたテキストから声帯のパラメータを推測し、声の元の信号を生成

　　　　　↓

声道のパラメータを推測し、音声が生成される過程をシミュレート

　　　　　↓

スピーカーから音を出す

このようにして音声が発せられる。音素は文脈や、有声音や無声音か？などといった質問から関数として表現される。質問によって関数が変化するから多様な声を表すことができ、歌詞や音程に関する質問をすれば歌わせることもできる。

名工大は他にも音素同士の繋ぎを滑らかにして喋らせるHTS(= H Triple S)の公開もしている。

第三章　「化ける」コンピュータ　---片思いの相手に話しかけてもらうには？

まずはX JAPANのhideさんの幻の曲「子ギャル」を聞いてみてほしい。

この曲はhideさんが亡くなってから発表された曲で、生前のhideさんを元にVOCALOID技術で声を再現している。違和感という違和感は感じられなかったであろう。

他にも、自分の好きな人に「君のことが好きだよ。」と言ってもらったり、私はミクちゃんに言ってもらったことがあるよ。

死んだお母さんの声をもう一度聞いてみたいだったり、アイドルに話しかけてもらいたいだったり。

音声合成の技術によってこれらは全て可能になるかもしれない。

ここでは平均声による話者適応についてまとめる。

平均声とは、多数の人の音声データをまとめた声のことである。多数の人からとっているため声の共通部分は強調され、声の個性部分は薄まる。これと先に述べたHMM音声合成を用いれば容易に特定の人の声を再現できる。

これに必要なのは、平均声から作られた関数と再現したい人の10分程度のサンプルデータの違いであり、平均声の関数をこの違いに元基づいて変換すれば望む声が得られる。

これを話者適応という。

平均声を用いないとしたら、再現したい人の声の収録に何時間もかかってしまう。

上記以外にも、暗い声や太い声などの特徴をパラメータとして表し声の関数に持ち込めば自在に操れるのもHMM音声合成の強みだ。

第四章　踏み越えるコンピュータ　---「声」の障碍と音声合成

ある日自分が喋れなくなったら、と想像したことはあるだろうか。

声帯が取れても自分の声で喋りたいよね。

今日、電気式人工喉頭という発声補助器具があるのは知っているだろうか。　

f:id:kigma:20190416162240p:plain — 電気式人工喉頭での発声 ※電動式人工喉頭　ユアトーンから引用(http://www.first-med.co.jp/products/yourtone.php)

上記のような物で低いブザー音と共に声が発せられる。10年位前に、私の知人のおじいさんがこれを使っていたが、ブザーの振動や速さが一定のため違和感が残った。

現在研究が進められている技術は「名探偵コナン」に出てくる蝶ネクタイのようなもので、

電気式人工喉頭と自分の体で作った不自然な音声

　　　↓

自分本来の声

上記の対応付けをHMM音声合成に似ているGMM(混合正規分布モデル)の統計モデルによって行う。音素と音素、音と音を対応付けているので、学習に使ったテキストは何でも良いのである。入出力の発話内容は変わらないと仮定しているので、抑揚や声色も変わらない。

ほぼリアルタイムでの変換が可能で、常に学習しているから期待できるシステムであろう。

現在では、多少のイントネーションの違いや疑問形など少しの抑揚が実現されている状況ではあるが、蝶ネクタイが完成するのはそう遠くないだろう。

第五章　話すコンピュータ　---言葉の壁を越える

ドラえもんの道具は実に夢がある道具がたくさんあるが、現代に「ほんやくコンニャク」があったら相当楽だろう。実際にそんなものがあるはずもなく、テレビとかに映る首脳会談では横に通訳が付いている状況だ。

しかし、大抵の通訳には専門的な知識があるわけでもないから「electron and hole (電子と正孔)」という英語を「電子と穴」と間違えて訳してしまうこともある。文脈を捉えることは人間でも難しいことであるしかり、機械でも難しいことなのだ。それでも翻訳技術は高まってきている。機械翻訳の流れとして、

翻訳元の音声を認識し、テキスト化

　　　　　　　↓

そのテキストを翻訳先のテキストに翻訳

　　　　　　　↓

翻訳先のテキストを音声化

上記に示した流れではあるが、自分の声で翻訳先のテキストを読み上げてもらうことには先に述べた平均声による適応を行う。アメリカ英語からインド英語への変換もその言葉の違いによって関数を変換すればよい。

日本人が日本人らしさを演出するときも、語尾が子音の時は若干の母音が付くことや、「th」が「s」に近い発音になることなど、その特徴に合わせた適応を行えばよい。専門用語もデータベース化していれば翻訳自体も済むのです。

これが実用化されてコンニャクの形になれば喋る前にお互いコンニャクを食べあう異様な光景が見れるかもしれないね（笑）。

第六章　おしゃべりなコンピュータの未来

音声合成技術が進歩して蝶ネクタイが完成してしまったら、振り込め詐欺として悪用される危険が出てくる。そこで合成音声と自然音声の違いを見分けることが必要になってくる。

合成音声では、人間には聞こえないがコンピュータでは見分けられる周波数成分はそれほどモデル化されていない。そこに注目しなくても人間らしい声は作れるからだ。逆に言うと、そこに注目すれば見分けられるというわけだ。現在でも9割ほどは区別できているらしい。

さらに向上を目指すべく、「自然な音声合成作りコンテスト」や「音声合成と自然音声を見破るコンテスト」と言ったこと行おうという機運が高まっている。これが実現できれば、「悪用は可能かもしれないが、悪用を防止する技術もある」といった音声合成にとってより良い環境ができるかもしれない。

音声合成は他にも、電車の中でぼそぼそと喋っていてもあいてが聞き取れる「サイレント音声コミュニケーション」や、気分によって声を変える声にとっての化粧、年を取っていても若いころの声を出せてしまえるといった様々な可能性がある。人間の仕事を奪うのではなく、分身として助け、人間と合成音声は共存している未来が見えるであろう。

おわり

音声合成の現状や技術、課題などをこの本で見てきたが、音声合成には無限の可能性を秘めていると感じた。音声合成について知らない人にもわかりやすく解説されており、とても面白かった。読んだことが無いなら読んでみてほしい。音声合成に対する価値観がきっと変わるだろう。