フーリエ〇〇をまとめてみた

こんにちは、きぐまだ。

デジタル信号処理の勉強をしているとふと、「あれ、フーリエ〇〇って何するんだっけ」となってしまうことがあるので、見たときにすぐ思い出せるように自分なりにまとめてみた。

公式の詳しい導出はこの記事では言及しないことにする。詳しく知りたい方は一番下の参照まで。

フーリエ級数
フーリエ変換
離散時間フーリエ変換
離散フーリエ変換
おわりに
引用・参照

フーリエ級数

公式

$\displaystyle f(t) = a_0 + \sum_{k = 1}^{\infty} \left\{a_k \cos{ \left(\frac{2\pi k}{T_0} t\right) } + b_k \sin{ \left(\frac{2\pi k}{T_0} t\right) } \right\}$

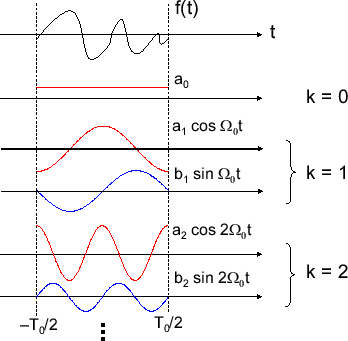
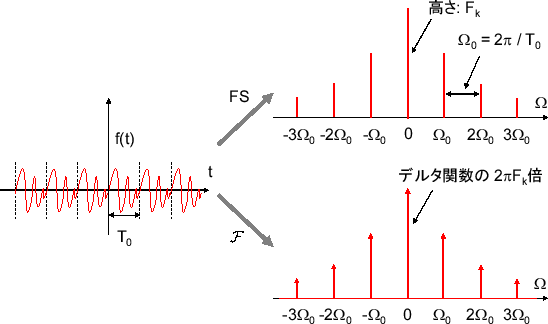
これは周期 $ T_0 $ の関数(信号)は角周波数が$ 2\pi / T_0 (= \Omega_0) $で自然数倍のsinとcosの足しあわせで構成されることを表している。$ a_0 $ は元の信号の振動しない成分だ。イメージは下の画像みたいな感じだ。

計算はしないのでフーリエ係数は省く。
フーリエ級数をオイラーの公式を用いて複素指数型で表すと、

公式

$\displaystyle f(t) = \sum_{k = -\infty}^{\infty} F_k e^{ j \Omega_0 k t}$

$\displaystyle F _ k = \frac{1}{T_0} \int_{-T_0 / 2}^{T_0 / 2} f(t) e^{-j\Omega_0 k t} dt$

$ F_k $ はこれのフーリエ係数を表している。
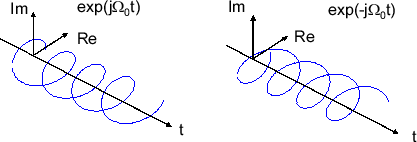
$ e^{ j\Omega_0 k t }$ は角周波数 $ \Omega_0 k$ の回転であり、反時計回りに時間と共に$ t $軸に進む。$ k < 0 $ の時は、時計回りに回転する。イメージは下の画像みたいな感じだ。

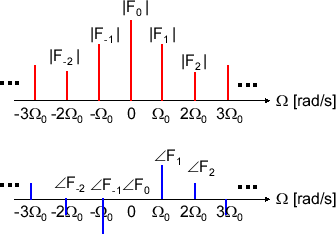
$ f(t) $ が実数だった場合、公式の複素数成分は無くならないといけない。つまり、$ F _ k e^{ j\Omega_0 k t}$と$ F _ -k e^{ -j\Omega_0 k t}$ の和が実数にならないといけない。よって $ |F _ k| = |F _ -k|$ の振幅が一致して、$ \angle F _ k = -\angle F _ -k $ の偏角の関係が成り立つ。フーリエ係数 $ F _ k $ が各周波数成分の振幅を表しているのでこちらのほうが直感的にわかりやすい。

フーリエ変換

公式

$\displaystyle f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(\Omega) e^{j \Omega t} d\Omega \ \ \ \ \ \ \ //フーリエ逆変換$

$\displaystyle F(\Omega) = \int_{-\infty}^{\infty} f(t) e^{-j \Omega t} dt \ \ \ \ \ \ \ //フーリエ変換$

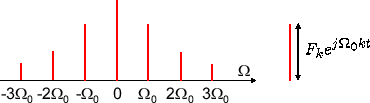
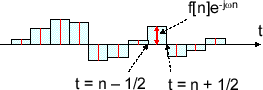
フーリエ逆変換は何となくフーリエ級数展開と似ていることがわかる。フーリエ級数展開では値が離散的だったが、面積として考え $ T_0 -> \infty$ すなわち $ \Omega_0 -> 0 $ としたものだ。そうすることで $ \Omega $ が連続化され積分で表せる。フーリエ変換も同様。面積のイメージは下の図みたいな感じだ。

　　　　　　　↓

そして、時間領域で周期的な $ f(t) $ をフーリエ変換すると、周波数領域ではデルタ関数が出てくる。これは周期関数を1周期だけ積分したフーリエ係数と違い、無限大まで積分するのでデルタ関数が出てくるのは必然だろう。周波数領域で見ると、フーリエ係数をフーリエ逆変換しても値を持たない。そこにデルタ関数をかけて面積を持つようにしてフーリエ逆変換すると、時間領域では信号が復元される。

離散時間フーリエ変換

公式

$\displaystyle F(\omega) = \sum_{n = -\infty }^{\infty} f[ n ] e^{-j\omega n} \ \ \ \ \ \ // 離散時間フーリエ変換$

$\displaystyle f[ n ] = \frac{1}{2\pi} \int_{-\pi}^{\pi} F(\omega) e^{j\omega n} d\omega \ \ \ \ \ \ // 離散時間フーリエ逆変換$

時間領域でただの離散的な値だと積分しても値が残らないので、先ほどのフーリエ逆変換と同じく面積として考えて総和を取ればよい。もしくは、離散的な値にデルタ関数をかけて値を持つようにすればよい。

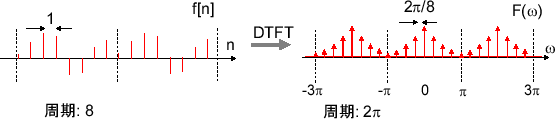
フーリエ変換では、離散的な周波数スペクトルは時間領域で連続だったが今回の場合、時間領域で離散的なので周波数スペクトルでは連続的になる。周期は $ 2\pi $ 。

周期的な周波数スペクトルをフーリエ逆変換すると、先ほど同様デルタ関数が出てくるので積分範囲は1周期だけにすると、離散時間フーリエ逆変換のようになる。だが、コンピュータが扱うことができるのはデジタル信号だけだ。そこで、周波数領域でも離散的な離散フーリエ変換が出てくる。

離散フーリエ変換

公式

$\displaystyle f[n] = \frac{1}{N} \sum_{k = 0}^{N - 1} F[ k ] e^{j \frac{2\pi}{N} k n} \ \ \ (n = 0 \cdots N-1) \ \ \ \ \ // 離散フーリエ逆変換$

$\displaystyle F[k] = \sum_{n = 0}^{N - 1} f[ n ] e^{-j\frac{2\pi}{N} k n} \ \ \ (k = 0 \cdots N - 1) \ \ \ \ \ // 離散フーリエ変換$

周期的ではない離散時間信号を離散時間フーリエ変換すると、周波数領域では周期 $ 2\pi $ の連続的なスペクトルになったが、時間領域で周期的だった場合、周波数領域では離散的になり、離散時間フーリエ変換では無限和とするので周波数領域ではデルタ関数が出てくる。

$ F(\omega) $ は

$\displaystyle F(\omega) = \sum_{k = -\infty}^{\infty} c _ k \delta(\omega - \frac{2\pi k}{N})$

と表せるから、離散時間フーリエ逆変換の式に突っ込んで色々変形すれば離散フーリエ逆変換が出てくる。

$ f[ n ] $ が周期的なとき、周波数領域ではデルタ関数が出てくるが、先ほど同様1周期分だけ総和を取ってしまえば値が無限にならなくて済む。つまり、$ \omega = 2\pi k / N $ の $ k = 0 \cdots N - 1 $ までの値が有限となって出る。これが離散フーリエ変換だ。

おわりに

どうしてこのような式になるのかを流れで理解するとそんなに難しいものではないことが分かった。

詳しい解説はぜひ参照から見てほしい。

引用・参照

・やる夫で学ぶディジタル信号処理(http://www.ic.is.tohoku.ac.jp/~swk/lecture/yaruodsp/main.html)